ON THE DEFINITION OF AN ACTUARIAL CLIMATE INDEX FOR THE IBERIAN PENINSULA
Abstract
Climate change is defined as a long-term shift in climate patterns affecting the planet globally. The main consequences of climate change are a rise in average temperatures in many regions, and an increase in the frequency and intensity of extreme weather events, such as floods, droughts, storms, or hurricanes. Climate change is associated also with a rise in sea levels, more frequent and severe wildfires, a loss of biodiversity, and many other disruptions with serious economic impacts. These new risks are increasingly affecting both the frequency and severity of claims in different insurance branches. To help insurance companies predict and manage these new risks, actuaries have defined the Actuaries Climate Index™ (ACI), which combines information from several important weather variables from historical records of the United States and Canada. The ACI shows a significant increasing trend over the years. It is important to note, however, that the impact of climate change is not the same in all parts of the planet: different regions and countries are affected in different ways. Therefore, it is important to check if the ACI is as useful to assess climate risk outside the United States and Canada. In this paper, we follow the North American ACI methodology in order to build an actuarial climate index for the Iberian Peninsula, which we call Iberian Actuarial Climate Index (IACI). The paper reviews in detail the methodology and the data used to obtain the IACI, and with it, studies the impact of climate change in the Iberian Peninsula.
El cambio climático se define como una transición en la tendencia a largo plazo del clima, que afecta al planeta globalmente. Las consecuencias principales del cambio climático son el alza de las temperaturas medias en muchas regiones, y el aumento de frecuencia e intensidad de eventos climáticos extremos, como inundaciones, sequias, tormentas, o huracanes. El cambio climático esta también asociado a la subida del nivel de los mares, a incendios forestales más frecuentes y severos, a la pérdida de biodiversidad, y varias catástrofes más, de impacto económico importante. Para ayudar a las compañías de seguros a predecir y administrar estos nuevos riesgos, los actuarios han definido el Actuaries Climate Index™ (ACI), que combina información de varias variables climáticas importantes proveniente de los datos históricos registrados en Canadá y Estados Unidos. El ACI exhibe una tendencia significativa al alza a lo largo de los años. Sin embargo, el impacto del cambio climático puede no ser el mismo en todas partes del planeta: diferentes regiones y países pueden ser afectados de forma diferente. Por lo tanto, es importante verificar si el ACI es útil para medir el riesgo climático fuera de Canadá e Estados Unidos. En este artículo seguimos la metodología del ACI norteamericano para definir un índice climático actuarial para la península Ibérica, que llamamos el Iberian Actuarial Climate Index (IACI). El articulo repasa en detalle la metodología y los datos utilizados para obtener el IACI, y con él, estudiar el impacto del cambio climático en la península Ibérica.
P alabras clave: Riesgo de cambio climático, Península Ibérica, Actuaries Climate Index™, Iberian Actuarial Climate Index, Red geográfica de alta resolución, España y Portugal
Keywords
Climate change risk, Iberian Peninsula, High resolution geographical grid, Spain and Portugal, Actuaries Climate Index, Iberian Actuarial Climate Index
Keywords
INTRODUCTION
Climate change refers to long-term changes in temperature, precipitation patterns, sea levels, and other aspects of Earth’s system. Climate change is one of the most complicated and pressing challenges that human society faces today, with heavy implications for the insurance industry because of its impact on increased frequency and severity in different lines of business. According to the Intergovernmental Panel on Climate Change (IPCC), the observed global surface temperature from 2011 to 2020 was 1.1 ℃ higher than the average in the last half of the 19-th century, with land surface temperature increasing by 1.59 ℃; see Ipcc (2023). Climate change poses a range of hazards and dangers, including more frequent and intense extreme weather events, rising sea levels that threaten coastal areas, water scarcity and droughts, disruption of ecosystems and loss of biodiversity, impacts on agriculture and food security, public health risks, significant economic consequences, and displacement and migration of populations.
For insurance companies, any increase in extreme weather events such as hurricanes, floods, wildfires, and droughts, that can cause significant damages would result in higher insurance claims. Moreover, if historical data are no longer representative due to changing weather patterns, insurers need to reassess the risk models they use and incorporate climate change projections and long-term climate risk assessments into their pricing to determine premiums accurately.
Review of the literature
At the end of the last century and the beginning of this century, the World Climate Research Program proposed several indices that could provide useful information on climate change; see Peterson, Folland, and Plummer (2001). In 2012, the Climate Index Working Group (CIWG) of the CAS Climate Change Committee summarised scientific knowledge on climate change, and proposed in a report to develop a composite index, termed the Actuaries Climate Change Index (ACCI), to include information from several climate variables, (Solterra Solutions, 2012). The development of the Actuaries Climate Index™ (ACI), which studies climate change in the United States and Canada, was proposed by this working group in 2014 and was launched in November 2016.
The Actuaries Climate Index™ was jointly developed by the Canadian Institute of Actuaries (CIA), the Society of Actuaries (SOA), the Casualty Actuarial Society (CAS), and the American Academy of Actuaries (AAA), from climate data in North America; see ACI (2018). It is intended to provide actuaries, public policymakers, and the general public with a neutral, factual and helpful climate change index monitoring tool, to learn about climate change and its associated risks. Just as the Consumer Price Index (CPI) tracks changes in the cost of a standard basket of goods and services over time, the ACI measures climate risks through a basket of extreme climate events and changes in sea level. The focus is on extreme weather events rather than averages; extremes have a greater impact on policyholders and their insured goods, as well as on society and the economy. The index consists of six components, each forming a monthly time series starting in 1961, from records of the National Oceanic and Atmospheric Administration (Menne, Durre, & Houston, 2012), GHCNDEX1 (Donat, Alexander, & Caesar, 2013), and the Permanent Service for Mean Sea Level (PSMSL, see Permanent Service for Mean Sea Level, 2023).
Curry (2015) investigates extending the use of the ACI formula to the UK and Europe. He reviews the ACI definition and methodology and finds that it applicable to this region without change, although it would need appropriate regional data.
In 2018, the Institute of Actuaries of Australia developed the Australian Actuaries Climate Index (AACI), using the ACI methodology, to monitor climate change in Australia; Aaci (2018). In addition,Nevruz, Atici, and Yi̇ldi̇rak (2022) propose to apply the ACI in Turkey, adapting it to the conditions in Ankara, developing an index suitable for this region. They suggest that choosing the best grid dataset for their ACI is more important than changing how the index is calculated. The ACI is designed to present climate trends to actuaries, policymakers, and the general public.
Pan, Porth, and Li (2022) investigate how effective the ACI is in predicting crop yields for (re)insurance ratemaking. They find that the ACI has significant predictive power for crop yields and yield losses, and argue that a high-resolution index could benefit the insurance industry. Most recently, in an oral presentation at the 80-th anniversary event of the Spanish Institute of Actuaries (IAE), a first draft defines a Spanish version of the ACI, over a shorter, more recent reference period than the ACI (1975-1995 in general and 1993- 2000 for sea levels). Their temperature variables also differ, using average highs and average lows, and the composite index formula. This index is not yet published, but some details can be found at IAE (2023).
Extension to Iberian climate data
Here the Iberian Peninsula is defined as the land area ranging from 36° to 43.7° north latitude and -9.5° to 3.3° east longitude, excluding France. Balearic and Canary Islands are not included in the data set. We calculate the Iberian Actuarial Climate Index (IACI) for the Iberian Peninsula using data from the ERA5-Land reanalysis dataset; see Copernicus Climate Change Service (C3S) Climate Data Store (CDS) (2022). Unlike the ACI for the United States and Canada which is calculated for 12 sub-regions, here we compute the IACI for a total of 6,526 cells forming the Iberian Peninsula grid; see Figure 1. The graph shows the approximate land inclusions of the grid cells along the borders and seacoast, and how the islands and other non-continental territories of Spain and Portugal are excluded from the IACI calculations.
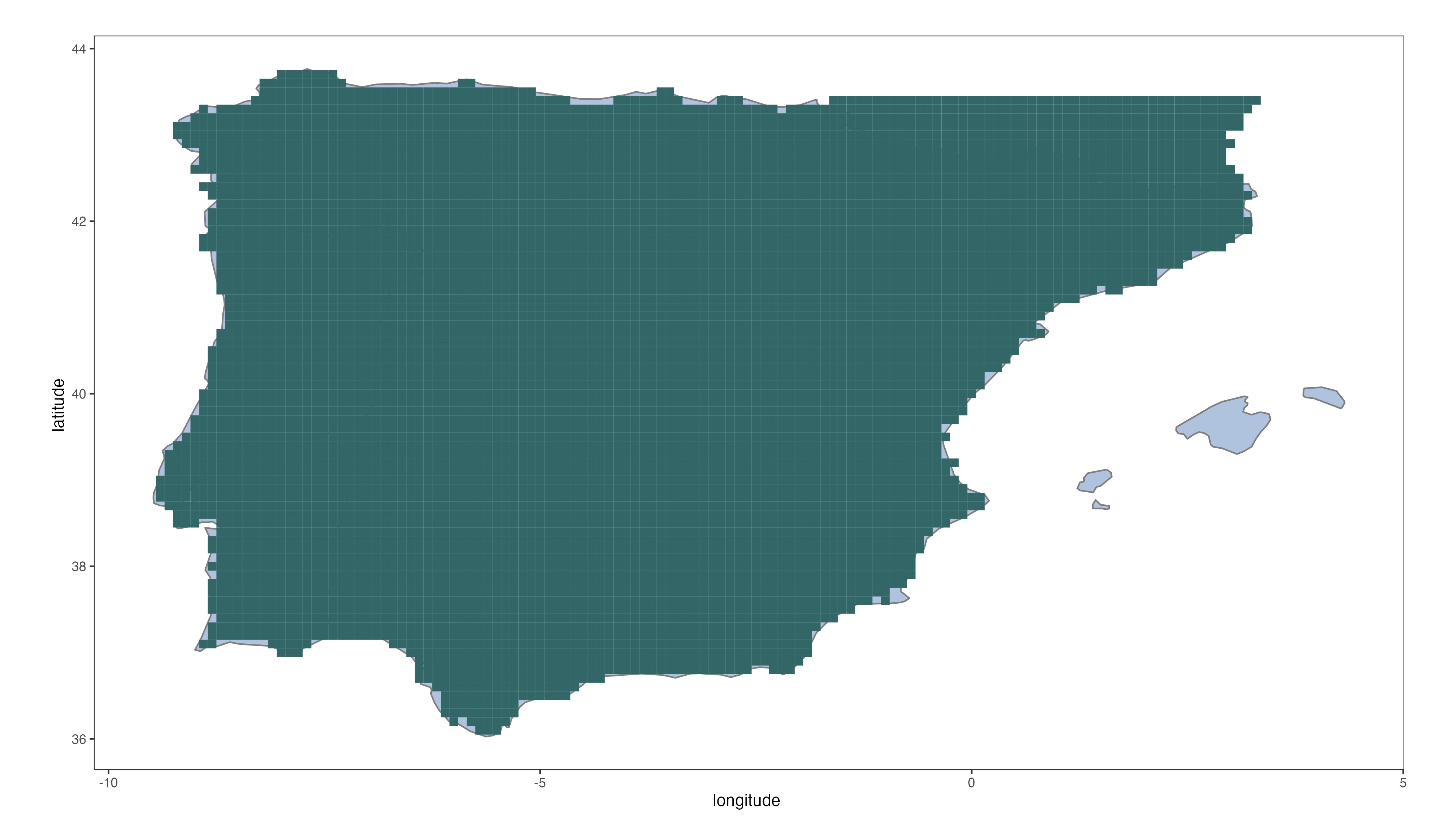
We compare the Iberian and North American cases and show how the IACI tracks well the climate change of the Iberian Peninsula through the years. You can see also the high-resolution IACI, showing the evolution of each grid by seasons through the years.
The rest of the paper is organised as follows. In Section 2 the Actuaries Climate Index™ (ACI) and its components are reviewed, discussing the possible application of the ACI to Iberian data, which is presented in Section 3. The comparison of the IACI with the North American ACI is presented in Section 4. Then, Section 5 splits and compares the IACI for Portugal to that of Spain. Finally, Section 6 gives a seasonal analysis of the IACI in each cell during the last 12 years. Some conclusive remarks and future developments wrap-up the paper.
THE NORTH AMERICAN ACTUARIES CLIMATE INDEX
Our purpose here is to extend to the Iberian Peninsula climate data the Actuaries Climate Index™ (ACI), originally defined for the United States and Canada. It was produced jointly by several actuarial societies in North America and combines six components, see Table 1, each of which is a monthly time series beginning in 1961. Hence, it is natural to first review the ACI methodology in detail, as it will help extend it to the Iberian Peninsula data.
|
Components |
Abbreviation |
Definition |
|
Warm temperature |
T90 |
Frequency of temperatures above the 90-th percentile |
|
Cool temperature |
T10 |
Frequency of temperatures below the 10-th percentile |
|
Precipitation |
P |
Maximum rainfall per month in five consecutive days |
|
Drought |
D |
Annual maximum consecutive dry days |
|
Wind speed |
W |
Frequency of wind speed above the 90-th percentile |
|
Sea level |
S |
Change in sea level |
The ACI uses a reference period from 1961 to 1990 as the basis to measure changes. The data from this period is used to calculate standardised anomalies for each component, relative to the reference period. The monthly-standardised anomaly is given by dividing the difference, between the value of each month and the average over the reference period, by the standard deviation of the reference period, like a Z-score.
The ACI is calculated monthly as well as on a seasonal basis in the same way (using meteorological seasons). It is determined by taking seasonal averages, for example, winter is the average of the calendar months of December, January, and February, then using the same standardising method as the monthly index.
Temperature components, T90, T10
The two temperature components are defined as the frequency of temperatures above the 90-th percentile and below the 10-th percentile, relative to the data from the reference period of 1961 to 1990. These frequency variables are detailed in Table 2.
For warm temperatures, because warmer days and warmer nights tend to occur together, the ACI measures the average of the percentage of days when daytime and nighttime high temperatures are greater than the corresponding 90-th percentile, centred on a 5-day window, over 1961-1990:
The cool temperature measure is calculated using a process similar to that used to calculate the frequency below the 10-th percentile:
where j = Jan, Feb, . . . , Dec, and k = 1961, 1962, . . . , 2022.
|
Notation |
Explanation |
|---|---|
|
TX90 |
Percentage of days when daily maximum temperature >90-th percentile of the reference period distribution for the relevant days |
|
TX10 |
Percentage of days when daily maximum temperature <10-th percentile of the referencie period distribution for the relevant days |
|
TN90 |
Percentage of days when nightly minimum temperature >90-th percentile of the reference period distribution for the relevant days |
|
TN10 |
Percentage of the days when nightly minimum temperature <10-th percentile of the reference period distribution for the relevant days |
As the climate warms, the occurrence of cooler extreme temperatures decreases, and the temperature distribution shifts to the right. Hence, the sign of T10 is reversed in the calculation of the ACI to correctly reflect the risk (increasing the ACI when T10 decreases). Fewer extreme cold events indicate that the climate is changing, affecting plant and animal ecology and weather patterns. Increased melting of permafrost, increased infectious diseases transmission, and populations of pests and insects that were previously less likely to survive cooler temperatures are all thought to be associated with a reduction in the frequency of extreme cold events.
The standardised anomalies for warm temperatures are calculated as the difference between the monthly frequency of warm temperatures > 90-percentile and the average monthly frequency of warm temperature during the reference period, divided by the standard deviation during the reference period. The warm temperature T90 and the cool temperature T10 use the same algorithm:
where j = Jan, Feb, . . . , Dec, and k = 1961, 1962, . . . , 2022, is the average monthly frequencies of warm temperature for all months during the reference period, is the standard deviation of warm temperature during the reference period.
The standardised anomalies calculation method for cold temperatures is consistent with that for warm temperatures:
where j = Jan, Feb, . . . , Dec, and k = 1961, 1962, . . . , 2022.
Precipitation component, P
The precipitation component focuses on extreme rainfall rather than average precipitation, using the maximum rainfall in any 5 consecutive days in the month, notated as . The percentage anomaly of maximum 5-day rainfall in a month, relative to the reference period value for a given month, is given by:
where j = Jan, Feb, . . . , Dec, k = 1961, 1962, . . . , 2022, is average in all months during the reference period, is the standard deviation during the reference period.
Drought component, D
Droughts are measured by the maximum number of consecutive dry days in each year, that is when the precipitation is less than 1 millimetre (denoted CDD(k)). Monthly values are obtained by linear interpolation of annual values:
The standardised anomalies calculations of CDD are similar to those for :
Wind speed component, W
Daily wind speed measurements are converted to wind power, WP, using the relationship WP (i, j) = 1/2ρw3, where w is the daily mean wind speed and ρ is the air density (taken to be constant at 1.23kg/m3). Wind power is used because the destructive potential of a wind has been shown to be related to wind power rather than wind speed. The wind component measures the monthly frequency of daily mean wind power above the 90-th percentile, denoted as WP 90.
The wind power thresholds are determined for each day i and month j in the reference period at each grid point separately. The thresholds value is determined as the mean plus 1.28 standard deviations of , for all 30 values of the same day and month in the 30-year reference period:
The count of days where mean winds exceed the threshold is then expressed as a percentage of the number of days in the month, providing an exceedance frequency measure, for every month of every year, throughout the entire period:
where i represents the day, j the month, k the year, and n(j) the number of days in month j.
Then the standardisation is as usual:
Sea level, S
Monthly mean sea level measurements can be obtained from tide gauges, which record changes in sea level relative to a vertical datum (to the sea floor). To avoid negative values, a revised local reference datum is defined to be approximately 7000 millimetres below mean sea level; see Permanent Service for Mean Sea Level (PSMSL) (2023). It is important to note that the height of the land relative to sea level is subject to change due to crustal movements, and these measurements encompass the combined effects of land and ocean positional changes. The standard anomalies in sea level are calculated using the following equation:
The composite ACI index
The standardised anomalies of these six components are averaged when they are combined into the Actuaries Climate Index, though the cool temperature is subtracted because the temperature probability distribution curve shifts to the right, as explained earlier:
IBERIAN PENINSULA DATASET
This paper defines the Iberian Actuarial Climate Index (IACI) calculations, using data from the ERA5-Land reanalysis dataset (Copernicus Climate Change Service (C3S) Climate Data Store (CDS), 2022) and tide gauge data obtained from the Permanent Service for Mean Sea Level; see Permanent Service for Mean Sea Level (PSMSL) (2023). All calculations are performed on each individual grid cell, and then the region-level indices for each component in the Iberian Peninsula are obtained by taking simple averages.
The ERA5-Land reanalysis data is a high-resolution dataset with a horizontal resolution of 0.1° x 0.1° for each grid cell. It was generated by replaying the land component of the ECMWF ERA5 climate reanalysis. Reanalysis combines model data with observations from various sources, including satellites, weather stations, and ocean buoys, to create a globally comprehensive and consistent dataset using the laws of physics; see M Muñoz-Sabater, Dutra, and Balsamo (2021). Unlike observational data, which may suffer from issues such as non-homogeneity and instrumental biases, reanalysis provides a more accurate representation of past climate conditions. The specific variables used in the analysis are shown in Table 3.
|
Name |
Units |
Description |
|
2m temperature |
k |
Ait temperature at 2m above the surface of land, sea, or in-land waters. Temperature mea-measured in Kelvin; convertible to degrees Celsius (ºC) by substracting 271.15. |
|
Total precipitation |
m |
Accumulated liquid and frozen water, includes rain and snow, fallen on Earth´s surface. Precipitacion variables do not include fog, dew or the evaporation in the atmosphere before landing on Earth. The units of precipitacion are depth in metres. |
|
10m u-component of wind |
m·s−1 |
Eastward component of the 10m wind. The horizontal speed of air moving eastwards, height of ten metres above Earth´s surface, in metres per second. |
|
10m v-component of wind |
m·s−1 |
Northward component of the 10m wind. The horizontal speed of air moving northwards, height of ten metres above Earth´s surface, in metres per second. |
The Permanent Service for Mean Sea Level (PSMSL) serves as a repository for tide gauge data, which is crucial for measuring long-term sea level changes; see Holgate, Matthews, and Pugh (2013). To ensure data quality, we specifically selected data from 20 tidal observatories along the Mediterranean and Atlantic coasts, around the Iberian Peninsula, and neighbouring countries (see the Appendix). By calculating the average value from these selected observatories, we obtained the sea level data for the Iberian Peninsula. Due to the nature of data collection, some tidal observatories may not have a complete time series of sea level data. In such cases, we did not include these missing data stations when calculating the average. For example, if only 5 out of the 20 stations provided data on a particular day, we calculated the sea level data for that day as the average value of these 5 stations. For this purpose, and to extend the data available in this averaging process, we have included some stations of the coasts of Portugal and France.
EXTENSION OF THE ACI TO IBERIAN DATA
The Iberian Actuarial Climate Index
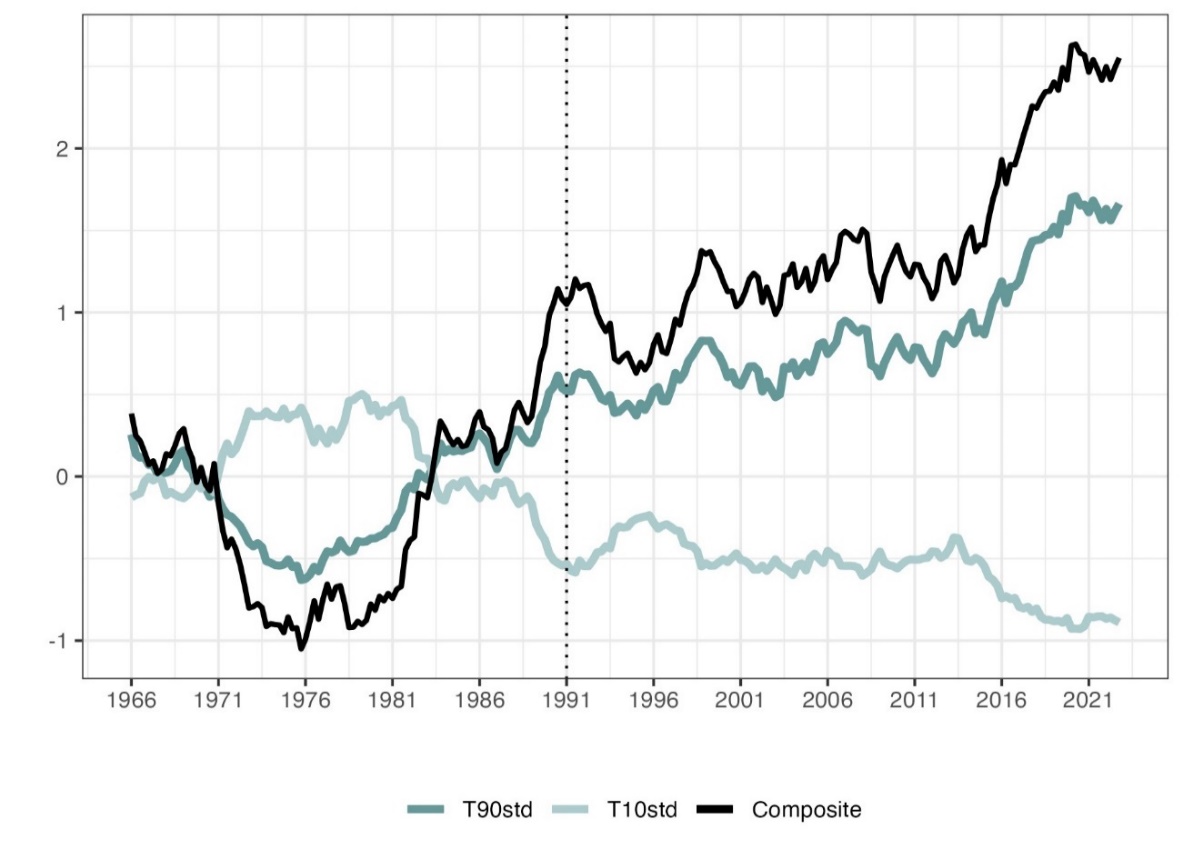
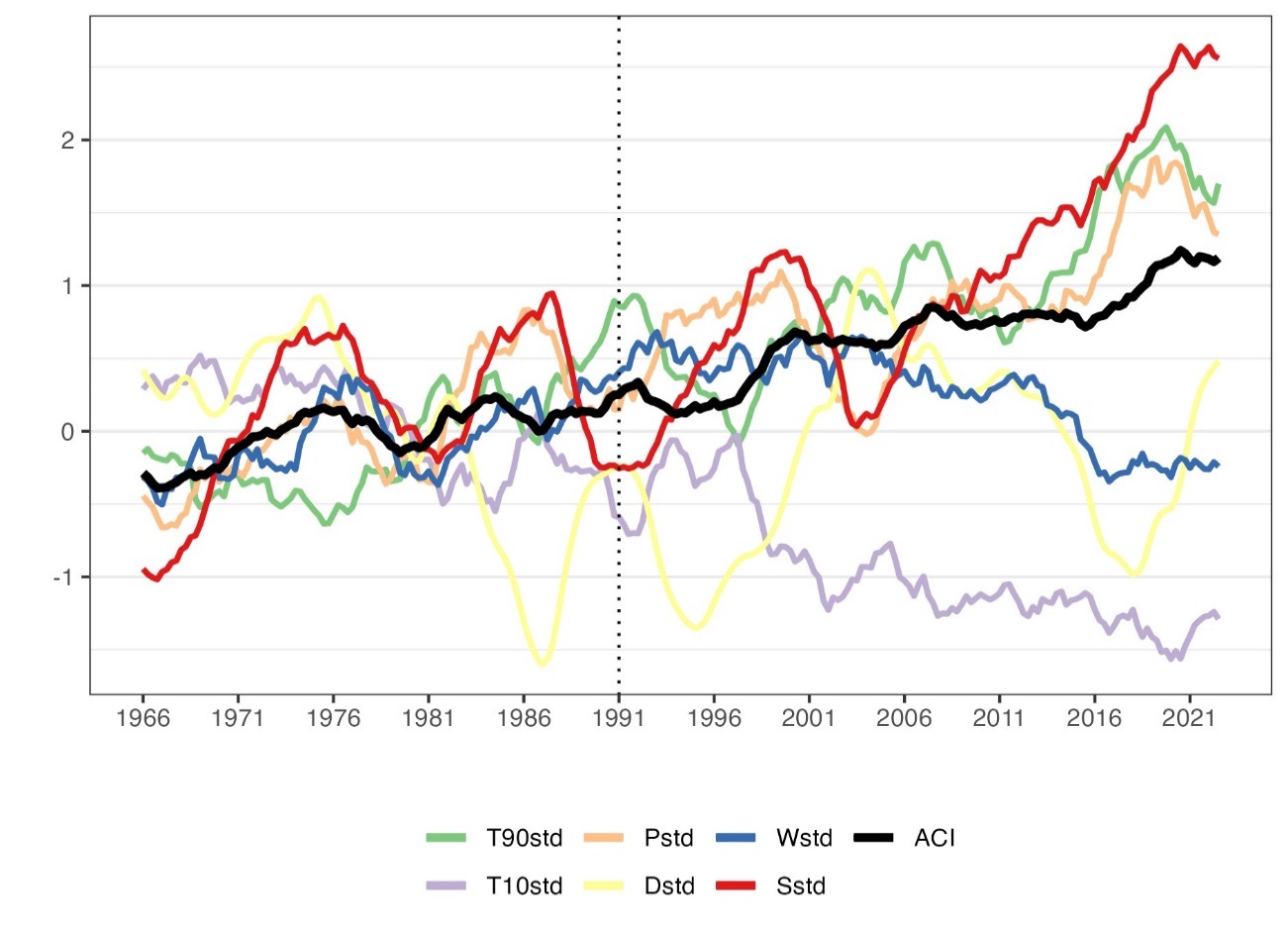
The warm and cool temperature components of each grid cell in the Iberian Peninsula (denoted IP in graph captions) are used to replace (1) and (2), respectively. The standardised anomalies of the temperature components, T90std and T10std, are from Equations (3) and (4).
The 5-year moving averages of these standardised anomalies are plotted in Figure 2, which depicts the changes in the frequency of extreme warm and extreme cold temperature events. It shows that the local cooling before the mid-1970s led to a decrease in the frequency of extreme warm temperatures and an increase in the frequency of extreme cold temperatures. Subsequently, climate change increased the frequency of extreme warm temperature events and decreased the frequency of extreme cold temperature events. This resulted in an increase in T90 and a decrease in T10, causing their difference to grow. The black line represents the 5-year moving average of T90std –T10std, which helps to better visualise the main trend. The change in the frequency of extreme warm temperature events is opposite to that of extreme cold temperature events, indicating that changes in air temperature have completely different effects on these two frequencies.
Then, Figure 3 illustrates the standardised anomalies of the precipitation component, Pstd, see (5). Positive values of the standardised anomalies show an increase in heavy precipitation events, compared to the reference period.
Conversely, when the value is -0.1, it means that the maximum 5-day rainfall has decreased by 0.1 standard deviations, relative to the mean of the reference period. From the figure, we see that heavy precipitation events on the Iberian Peninsula have slightly decreased compared to the reference period.
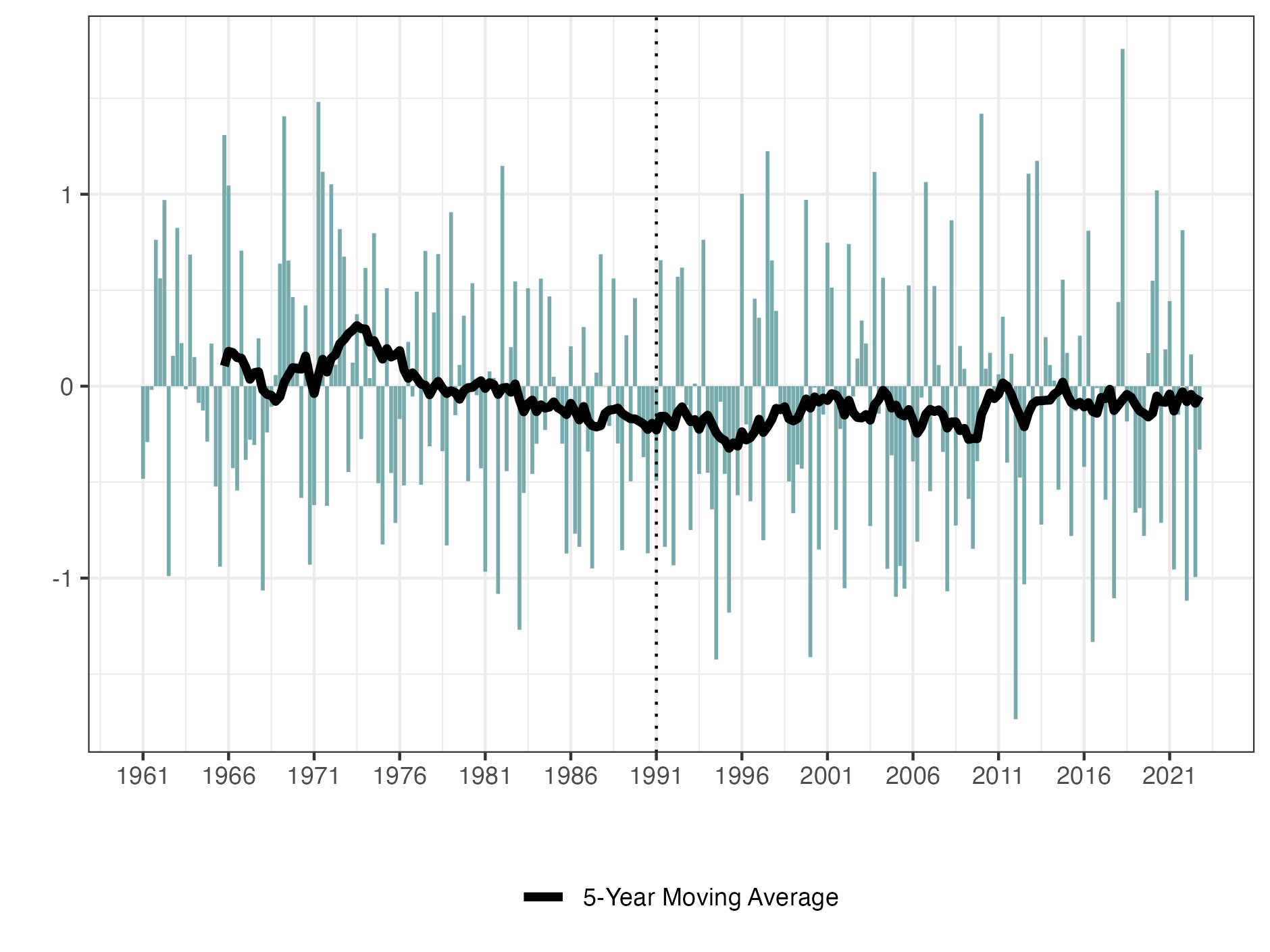
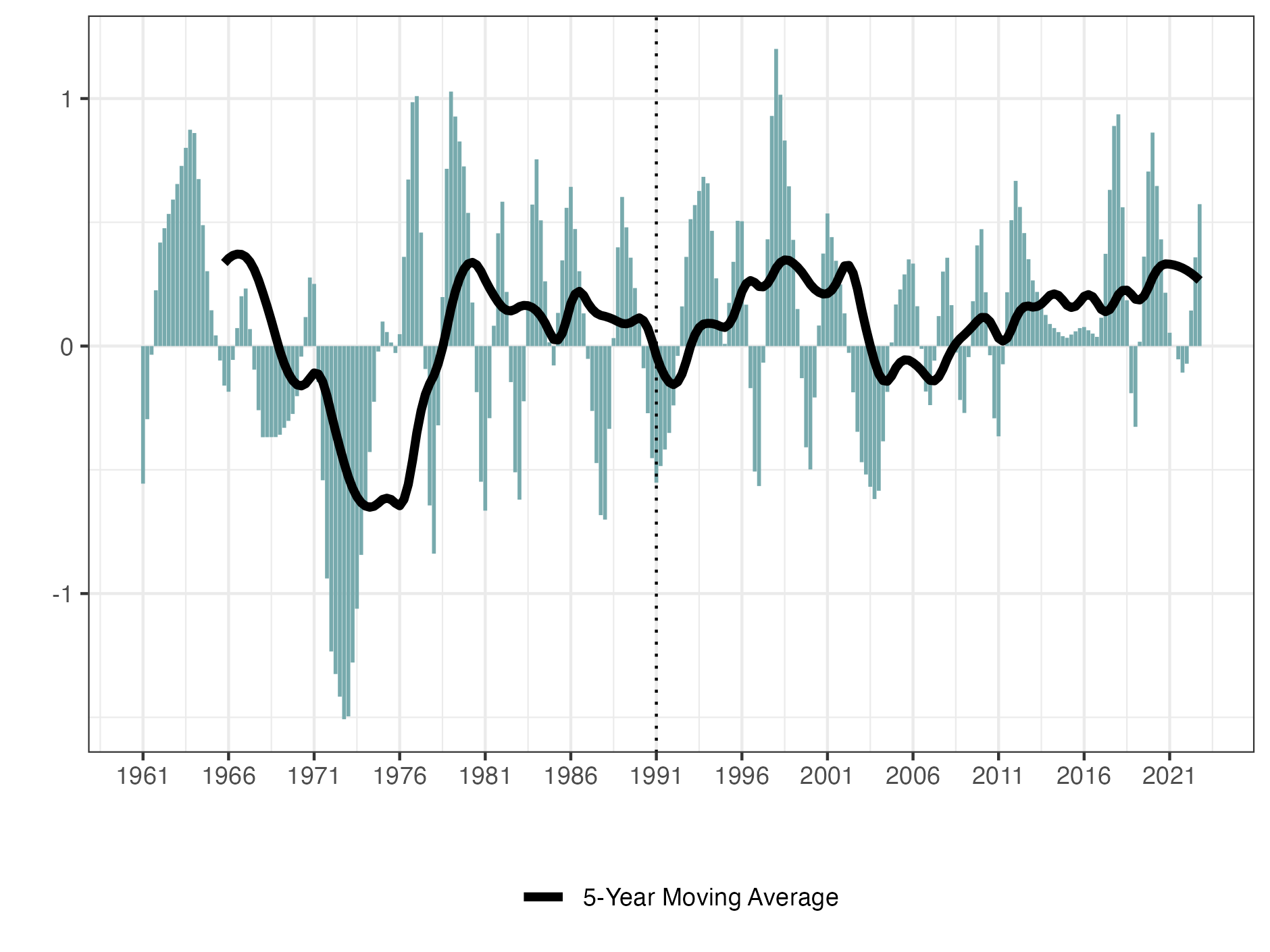
Figure 4 plots the Dstd time series, see Formula (7), representing the maximum consecutive dry days in the Iberian Peninsula. From the figure, it is clear that the maximum consecutive dry days have increased, in comparison to the reference period. This indicates longer periods without rainfall in the region. Furthermore, considering the monthly maximum five-day precipitation, shown in Figure 3, one can gather additional insights. The figure demonstrates that heavy precipitation events, as measured by the P component, have decreased slightly in the Iberian Peninsula, compared to the reference period. This implies a reduction in the amount of precipitation during such intense rainfall events. Combining these observations, we can infer that the Iberian Peninsula is experiencing a trend toward drier conditions. The increased occurrence of consecutive dry days, along with the decrease in heavy precipitations, suggests a shift towards reduced overall rainfall and an overall increase in dryness in the region.
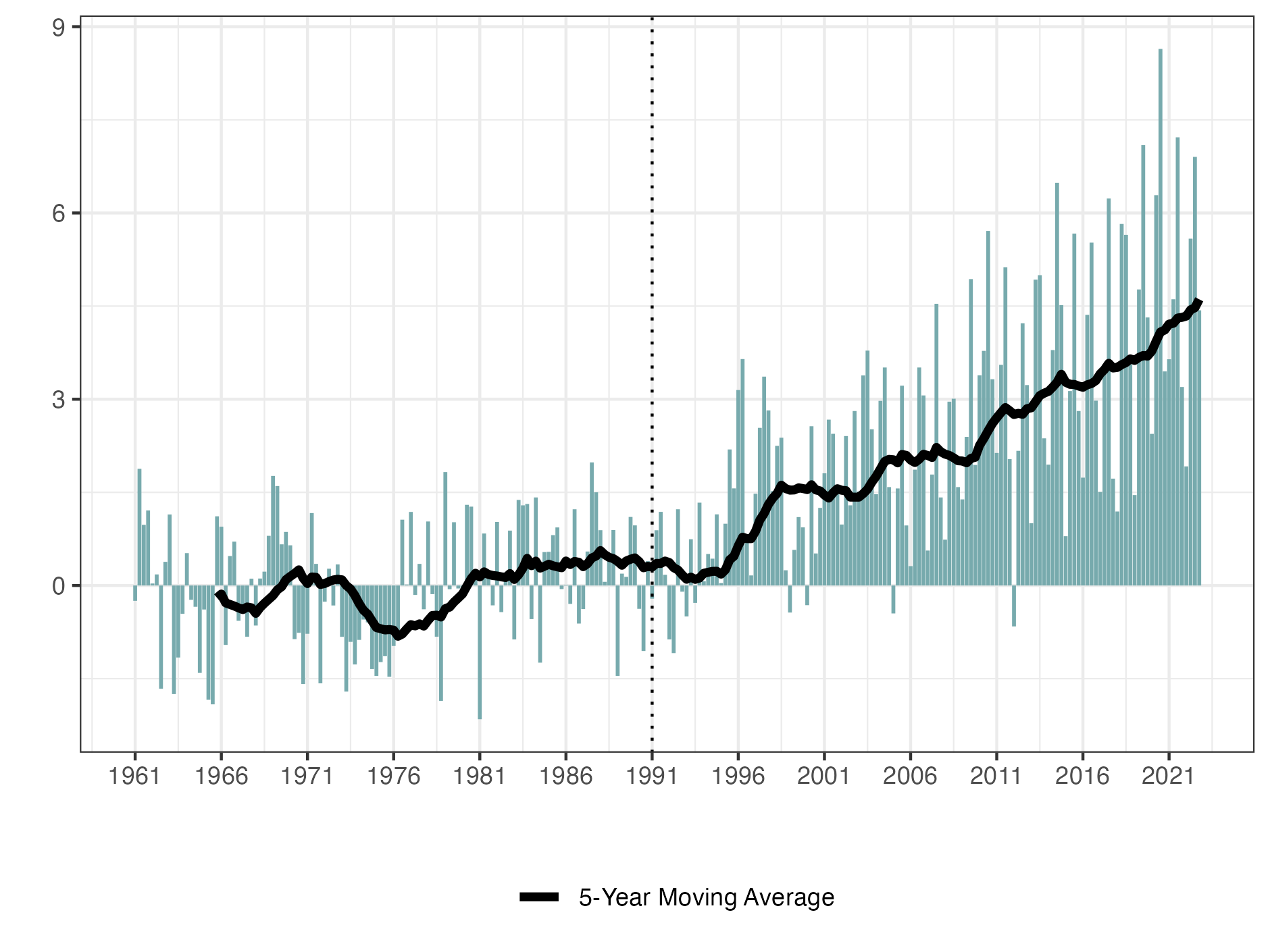
Next, Figure 5 shows the changes in wind power in the Iberian Peninsula, which seems to have a similar trend to that of wind speed. From this figure, we can assume that, in general, winds in the Iberian Peninsula reach higher speeds after than during the reference period. Interestingly, the figure also suggests some kind of periodic trend in wind speeds in the Iberian Peninsula.
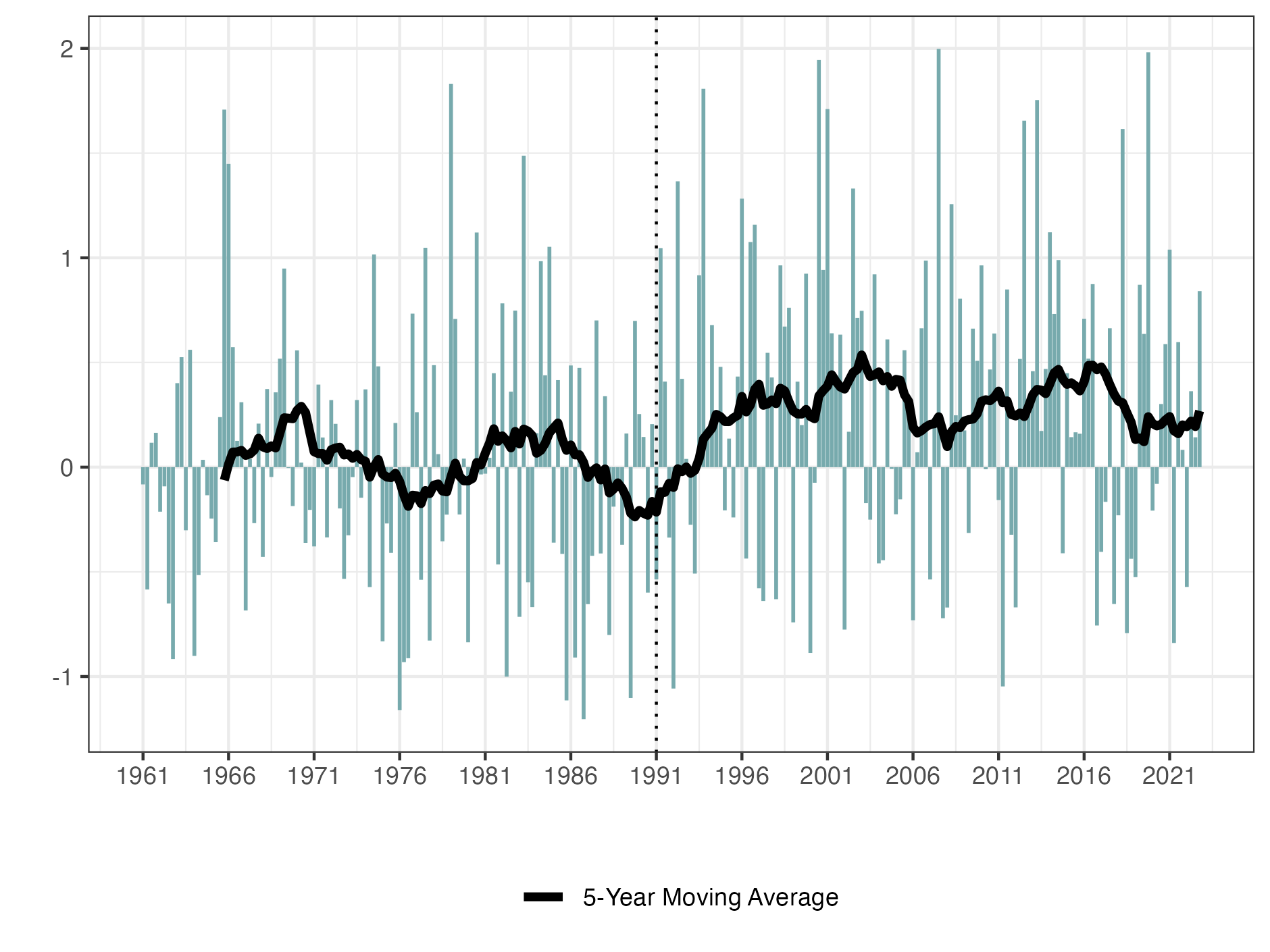
Finally, Figure 6 shows the seasonal standardised anomalies of sea level in the Iberian Peninsula. The value △S = S(j, k) − µref (j) has been positive since 1991 and has progressively increased over time. These findings indicate that, in general, the sea level around the Iberian Peninsula is rising yearly. The warming of the earth’s climate has melted ice sheets and glaciers, and the thermal expansion caused by warming seawater has further exacerbated sea level rise. Rising sea levels imply a series of risks for coastal areas of the Iberian Peninsula, such as coastal erosion, flooding, and salinisation of freshwater resources.
Curry (2015) uses a factor fS as the fraction of the number of coastal to total grid points, 0 < fS ≤ 1, to adjust the ACI as follows:
Considering the specificity of the geographical location of the Iberian Peninsula, we argue that the sea level variable S is important for the entire region. Hence, for now, we set fS = 1, as in the ACI, and defer to future work the study of estimating fS as in Curry’s extension of the ACI to the UK. The Iberian Actuarial Climate Index (IACI) for the whole Iberian Peninsula, given in (13), is hence obtained by averaging the IACI values from each grid cell.
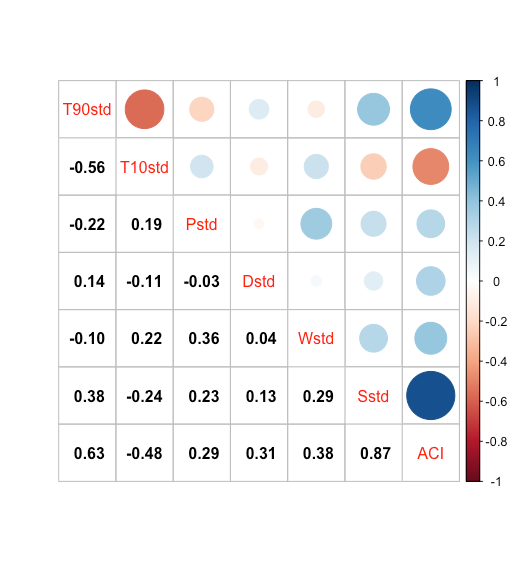
Figure 7 reports the correlation coefficients between the IACI and its 6 components. As anticipated, the correlations among the components are generally weak, except for the frequency of extreme warm and extreme cool temperatures, which exhibit a notable association. Moreover, there is a significant positive correlation observed between the IACI and sea level changes, as well as the frequency of extreme warm temperatures.
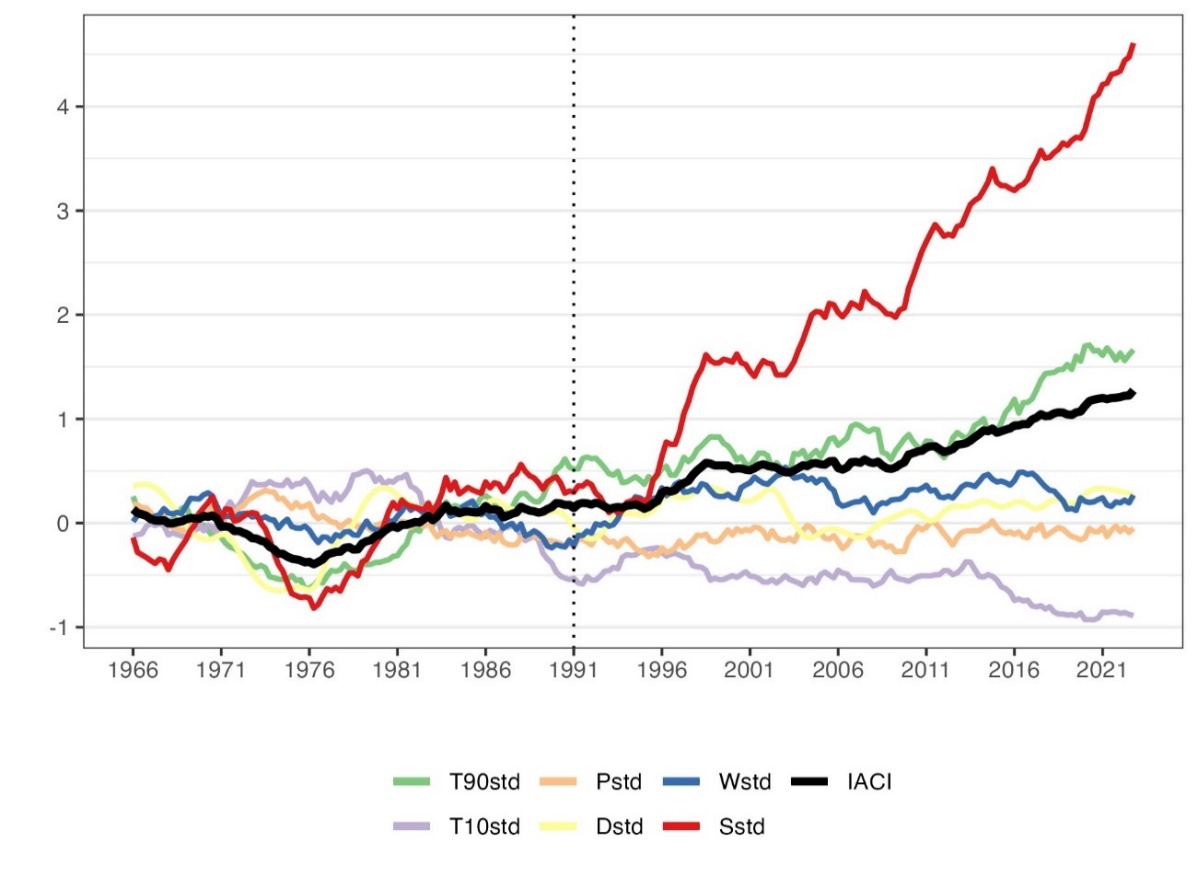
Finally, Figure 8 shows the 5-year moving average of the seasonal IACI and its 6 components. The sign of the IACI is determined mainly by the sea level and the frequency of extreme warm temperatures. A positive IACI value means an increase in the included climate extremes since 1991, relative to the 1960-1991 reference period. The value is expressed as a standardised anomaly, implying that a component index of 0.5 means that the component has increased on average by 0.5 standard deviations. The IACI clearly shows that climate extremes in the Iberian Peninsula have become more frequent, compared to 1960-61.
Comparison with the North American ACI
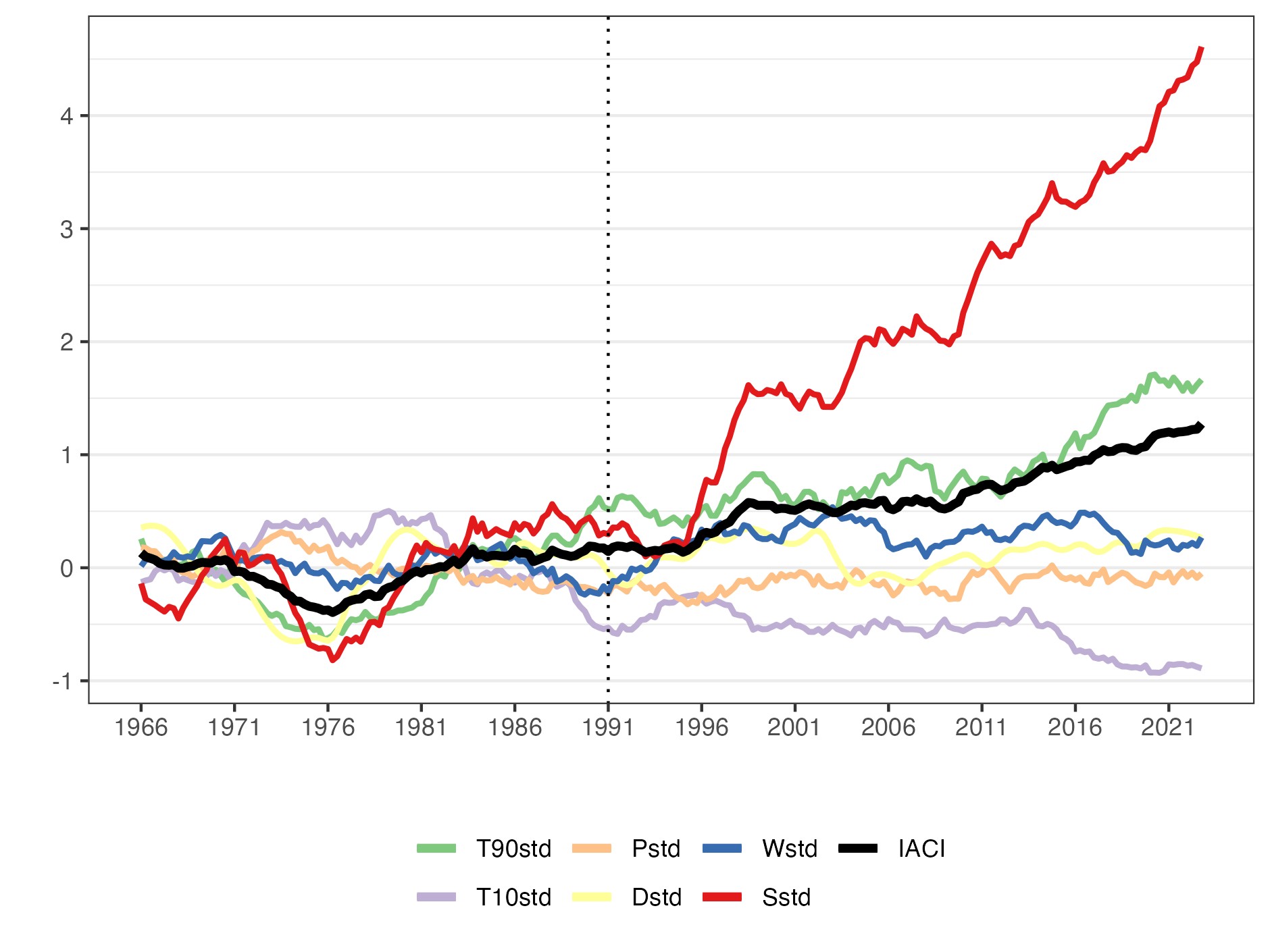
Figure 9 shows the seasonal Actuaries Climate Index™ of the United States and Canada (here denoted as USC) from 1961 to 2022. Compared to the Iberian IACI, both have similar trends in temperature components (T90std, T10std), although their values are different. After to the reference period, the frequency of extreme warm temperature events in the United States and Canada is higher than in the Iberian Peninsula.
Unlike the small decrease observed in the Iberian Peninsula, North America experienced a significant increase in maximum five-day precipitations (Pstd) after the reference period. Furthermore, its increasing trend shows some periodicity. The land areas of the United States and Canada are very large; hence, each region has different dry periods. Overall, the USC drought component (Dstd) does not show a clear trend. However, the USC average annual maximum consecutive dry days, since the reference period, is slightly smaller. The trends in the precipitation (Pstd) and drought (Dstd) components indicate that the USC has become wetter, compared to the IP.
Another difference with the Iberian Peninsula, wind speeds in the United States and Canada did not change significantly during the post-reference period, and these wind speed changes are different for each region in the USC. The Actuaries Climate Index™ website provides regional graphs of the ACI and of its 6 components for the USC and its 12 sub-regions 1 .
Sea level changes show a similar increasing trend in both the Iberian Peninsula and the USC. However, the sea level change data in the USC indicates that not all regions, within these countries, experience a sea level rise. In fact, some areas have sea levels lower than the 1961-1990 reference period average-level. In addition, some inland regions are not affected by sea level changes. These regional differences cause their average, that is, mean sea level change in the USC, to change less than in the seas around the IP.
Although the performance of each component of the Actuaries Climate Index™ and the Iberian Actuarial Climate Index is not exactly the same, due to the differences in geography, their composite index shows a similar increasing trend. Moreover, the values are also similar, ranging from -0.5 to 1.5. Particularly in recent years, their composite index values have consistently exceeded 1. This indicates that climate change has led to a similar factor of the standard deviation increase in the frequency of extreme weather events, both in the Iberian Peninsula and USC, compared to the 1961-1990 reference period. In summary, the occurrence of extreme climate events is becoming increasingly common in these two regions.
SEPARATE IACI FOR SPAIN AND PORTUGAL
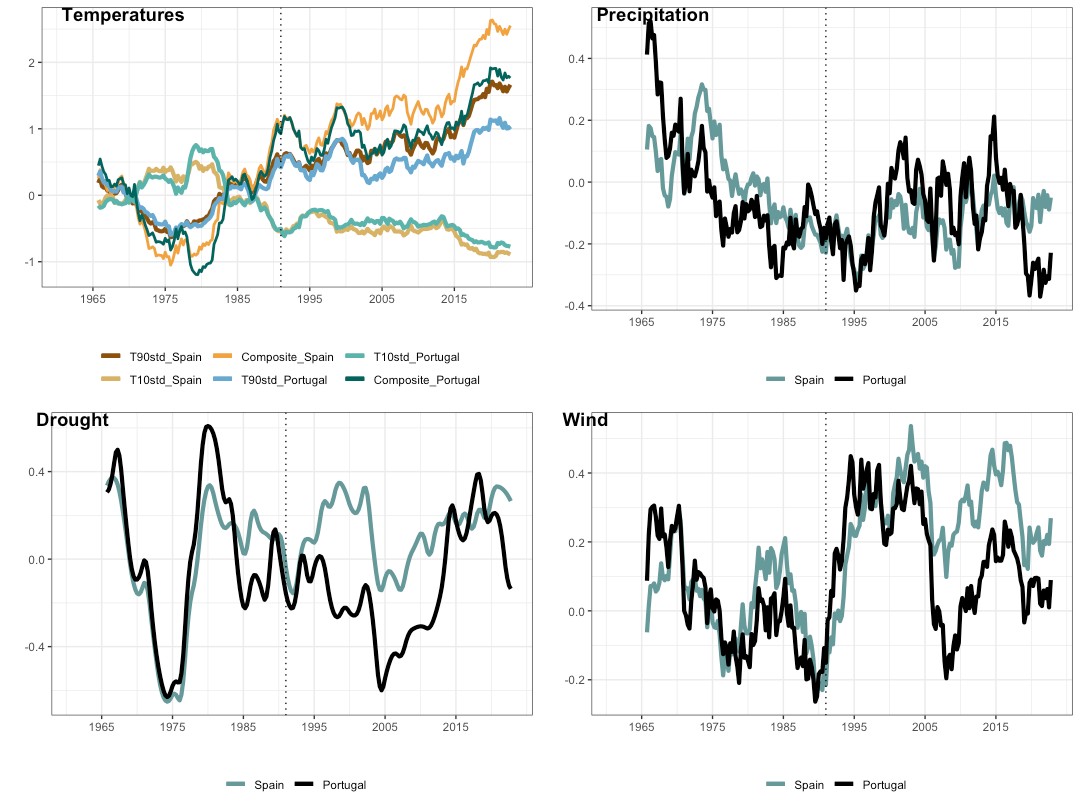
From this temperature components figure, we see that the frequency of extreme cold temperatures is similar in both countries of the IP. However, the frequency of extreme warm temperatures in Spain (brown line) is higher compared to that of Portugal (blue), indicating that extreme warm temperature events occur more often, since the reference period, in Spain than in Portugal.
Simultaneously, we observe that the standardised anomalies of the maximum 5-day precipitation in Spain are mostly below zero. Meaning that this component is generally lower in value after the reference period than during 1961-1990. In Portugal, this change has started to occur more recently. In addition, Spain has more consecutive dry days per year, after, than during the reference period, while Portugal does not show a significant change. These differences show that even if both countries are located in the Iberian Peninsula, only Spain seems to be getting drier.
The wind component, also plotted in Figure 10, shows an increasing trend of wind speeds in Spain, while there is no similar clear trend in Portugal.
Note that the sea level variable Sstd is calculated by combining measurements from 20 tide-gauge stations located along the Mediterranean and Atlantic coasts close to Spain and Portugal (including one in Ceuta and 7 in France). Calculating this variable separately only for Portugal would not produce credible means as the time series of sea level data from some tidal stations is not complete. Hence, the two red curves in Figures 11 and 12 are identical.
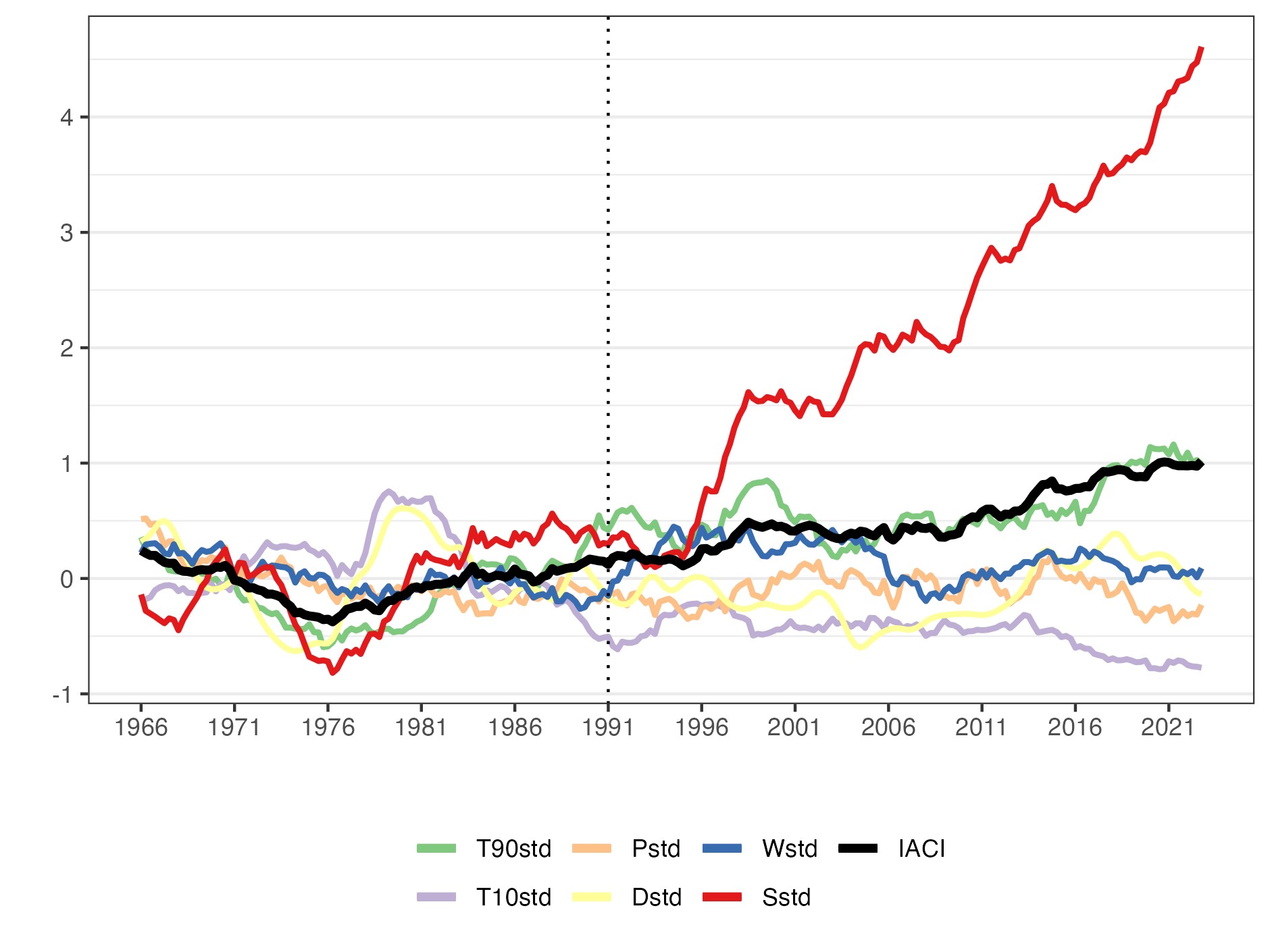
In summary, both countries are being affected differently by climate change. Spain is getting drier and hotter since the reference period, as further illustrated in Figures 11 and 12. Portugal’s IACI is slightly lower in value than that of Spain, indicating a relatively lower impact of climate change in Portugal compared to Spain. Finally, Figure 11 shows also that Spain is experiencing more frequent extreme climate events than Portugal. We can conclude that national differences need to be considered when assessing climate risk in the Iberian Peninsula.
HIGH-RESOLUTION SEASONAL IACI FOR RECENT YEARS
Figures 13 to 15 show the evolution of the seasonal IACI over the years 2011-2022 at a high (cell-level) resolution. Extreme climate events seem to occur more frequently during the summer, across most of the Iberian Peninsula. In many locations, the index reaches values of approximately 3. At a single component level, this would mean that the index has increased by an average of 3 standard deviations over the reference period average. For the composite IACI, combining all 6 components, the interpretation is not as straightforward, as the standard deviation of the average
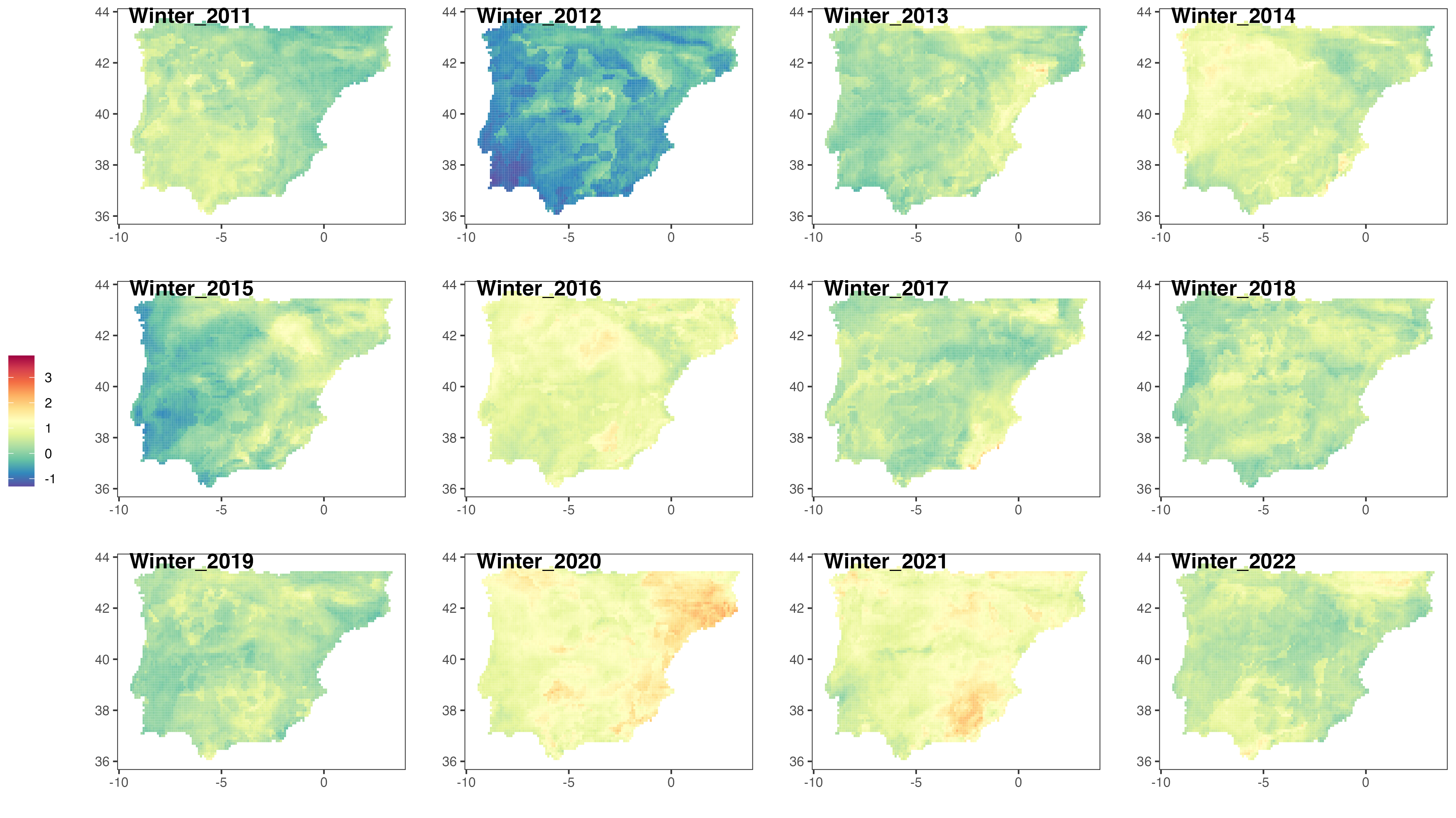
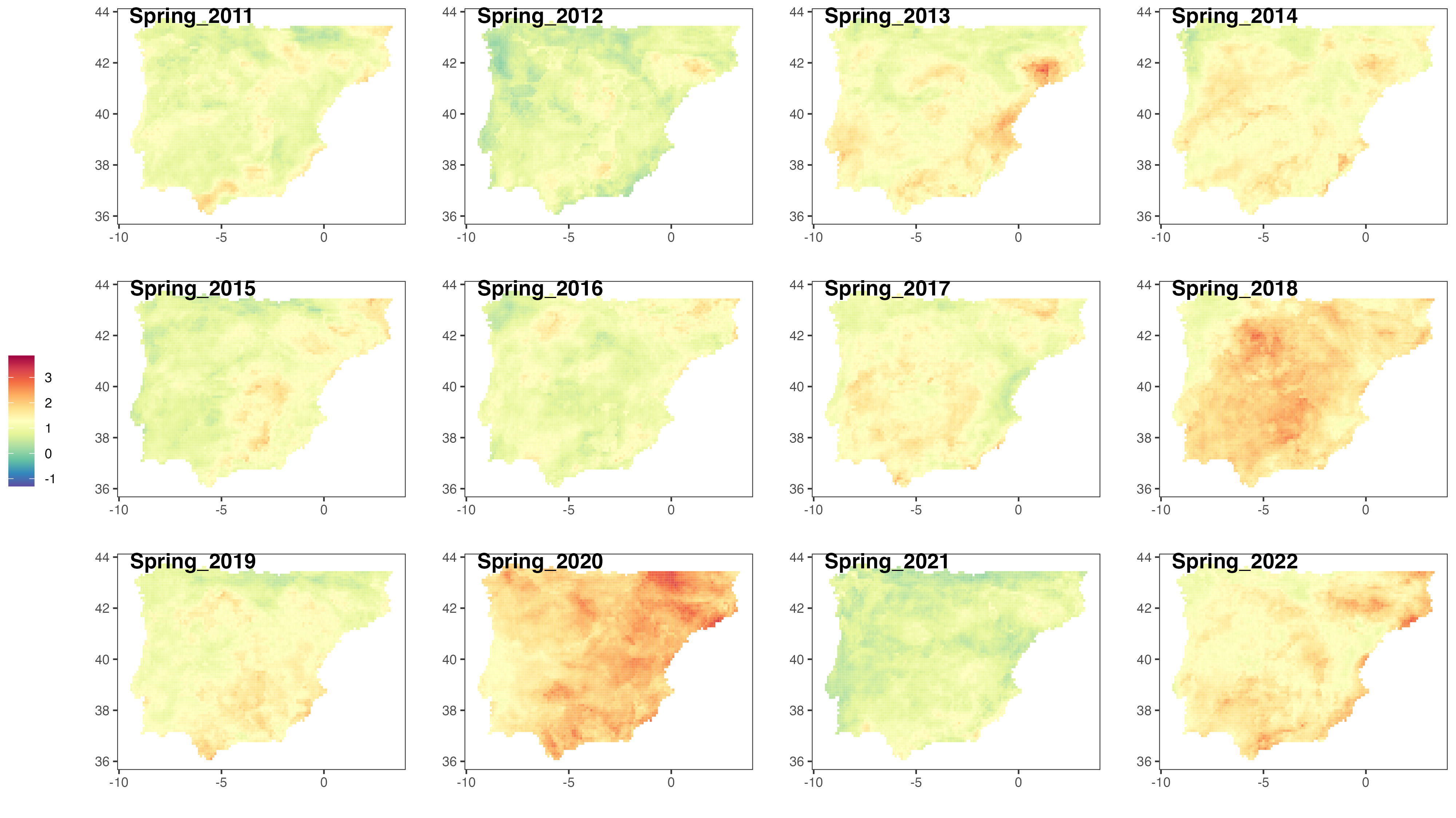
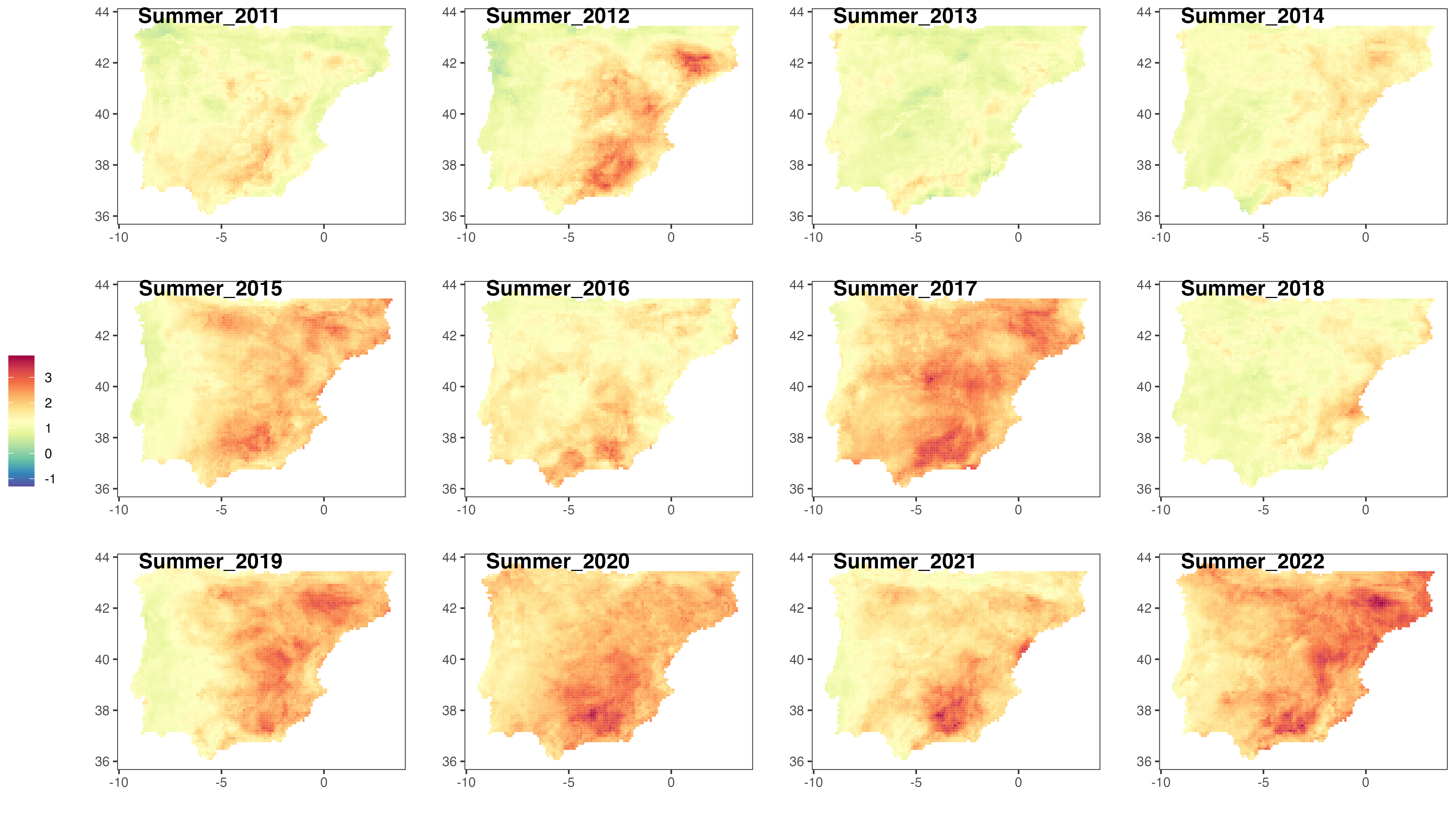
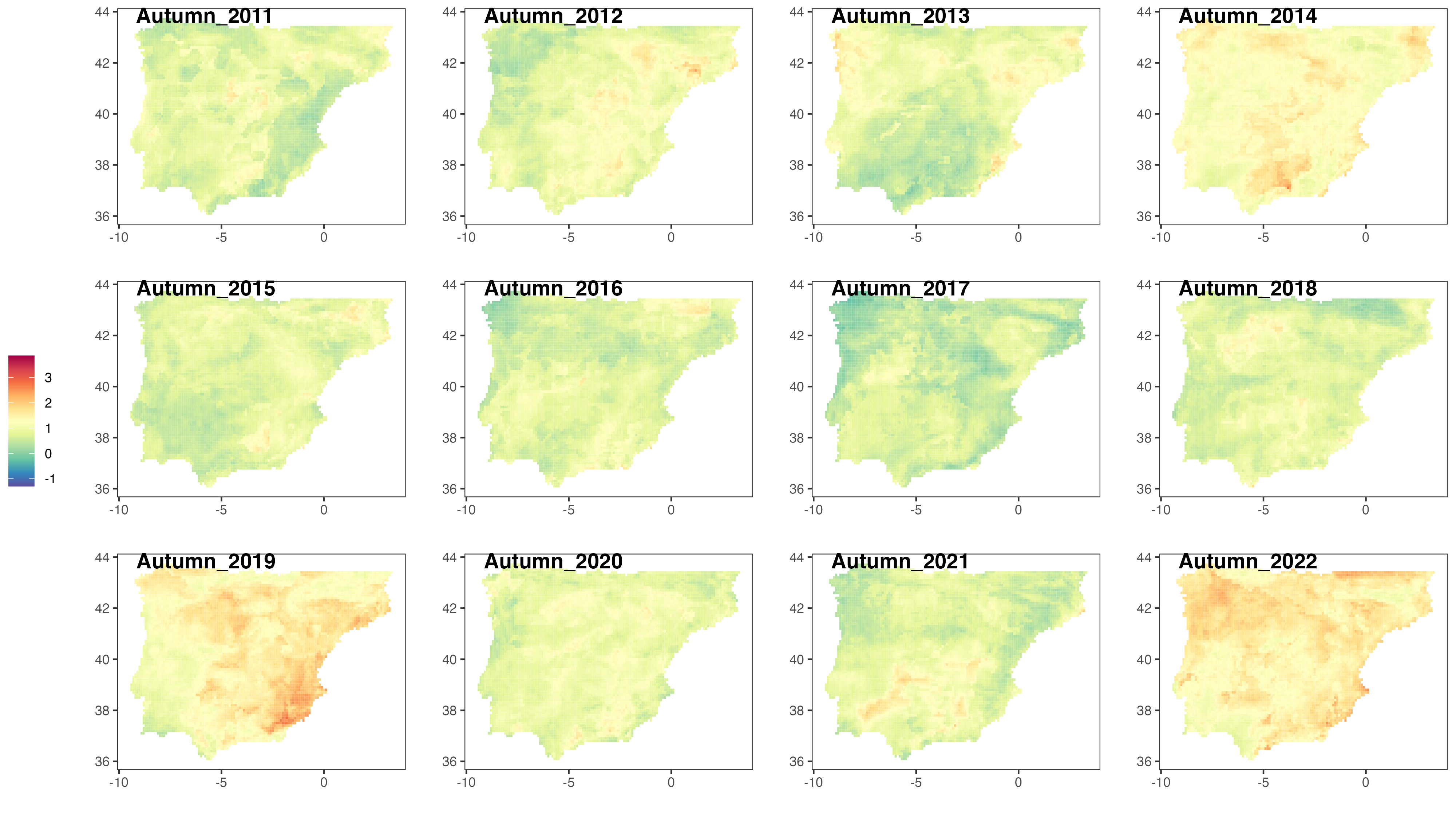
Furthermore, it is clear again from the figures that Portugal, in the western part of the Iberian Peninsula, is less affected by climate change, compared to Spain. Over the past 12 years, the Iberian Actuarial Climate Index (IACI) values of the cells within the geographical range of Portugal have consistently remained around 0, regardless of whether it is summer or winter.
Note, however, how the evolution of the IACI varies across different cells within a region. Each individual grid cell is affected by climate change in a unique manner. This means that the impact of climate change in each specific area may differ. This heterogeneity also implies that the frequency of extreme climate events varies per region. This could indicate also that the level of vulnerability and/or adaptability to extreme weather conditions can differ from one cell to another.
CONCLUSION
Due to the effect of climate change, forecasts from historical data become less reliable when quantifying insurable risks. Hence, insurance companies need to revise their risk models to account accurately for climate-related risks. This can be done through climate model forecasts and long- term climate assessment factors. The Iberian Actuarial Climate Index (IACI), which is based on the methodology of the North American Actuaries Climate Index™ (ACI) for climate data from the Iberian Peninsula, provides a comprehensive, objective and reliable summary of the region’s extreme climate changes.
Comparisons between the IACI and the ACI for the United States and Canada (USC) reveal very similar trends, suggesting a consistent pattern of extreme climate change in these two regions. On the other hand, when examining the data for specific sub-regions within either the United States and Canada or the Iberian Peninsula, it appears that the nature of these extreme climate event changes varies within large areas. This is in part because the aggregation of a fewer number of cells (maybe disjoint in the definition of some sub-regions), can result in quite different mean values and standard deviations, both integral parts of the definition of the IACI. To capture these non-homogeneous climate risks, the IACI is calculated here over 6,526 cells.
Sub-regions inside the Iberian Peninsula can be studied from a simple aggregation of the appropriate cell subsets. This approach enables the assessment of extreme climate trends at a higher resolution, more localised level, providing insurance companies with a precise tool for quantifying climate risk.
Using the IACI and its cell-level insights, insurers can improve their understanding of the specific climate risks faced by different areas within the Iberian Peninsula and make more accurate assessments when determining premiums and managing their overall risk portfolios.
Future research will investigate whether the IACI index can be improved by means of a different selection/definition of its current components. Also, the definition of the grid cells and the resulting sub-regions (based on political, geographical, meteorological, or even risk-oriented divisions) needs to be revisited, to better bridge the physical climate risk with the impacted financial insurance risks. The ultimate goal is to add an IACI to our actuarial toolbox that helps quantify and manage claim frequency and severity, excess mortality, excess morbidity, climate risk-adjusted premiums and reserves, or other relevant actuarial applications.
ACKNOWLEDGEMENTS
The authors are thankful to the participants of the 26-th IME Congress for their constructive comments on this project. Prof. Garrido gratefully acknowledges the partial financial support of NSERC grant RGPIN–2017–06643. Prof. Vilar-Zanón and Prof. Heras worked under projects PID2020-115700RB-I00 and PID2021-125133NB-I00 sponsored by the Spanish Government Ministry of Science and Innovation.
Appendix
List of tide gauge stations
|
Station name |
ID |
Lat. |
Lon. |
Time span of data 2 |
Completeness (%) |
|
|
ALICANTE 1 |
208 |
38.338 |
-0.478 |
1952 - 2020 |
75% |
|
|
ALICANTE 2 |
960 |
38.339 |
-0.481 |
1960 - 2020 |
93% |
|
|
CARTAGENA |
1460 |
37.597 |
-0.974 |
1977 - 1987 |
84% |
|
|
CEUTA |
489 |
35.892 |
5.316 |
1944 - 2018 |
96.6% |
|
|
L’ESTARTIT |
1764 |
42.054 |
3.206 |
1990 - 2022 |
100% |
|
|
MALAGA |
496 |
36.713 |
-4.415 |
1944 - 2013 |
82% |
|
|
MALAGA 2 |
1810 |
36.712 |
-4.417 |
1992 - 2021 |
96% |
|
|
BOUCAU |
1801 |
43.527 |
-1.515 |
1967 - 2022 |
82% |
|
|
BREST |
1 |
48.383 |
-4.495 |
1807 - 2022 |
90% |
|
|
CADIZ 2 |
209 |
36.528 |
-6.311 |
1880 - 1990 |
42% |
|
|
CADIZ 3 |
985 |
36.540 |
-6.286 |
1961 - 2018 |
97% |
|
|
CASCAIS |
52 |
38.683 |
-9.417 |
1882 - 1993 |
93% |
|
|
LA CORUÑA 1 |
484 |
43.369 |
-8.398 |
1943 - 2018 |
98% |
|
|
LEIXOES |
791 |
41.183 |
-8.700 |
1956 - 2022 |
76% |
|
|
POINTE ST. GILDAS |
1078 |
47.133 |
-2.250 |
1964 - 1988 |
91% |
|
|
PORT BLOC |
1915 |
45.569 |
-1.062 |
1964 - 1988 |
91% |
|
|
PORT TUDY |
1247 |
47.644 |
-3.446 |
1975 - 2022 |
93% |
|
|
ROSCOFF |
1347 |
48.718 |
-3.966 |
1973 - 2022 |
94% |
|
|
SINES |
1456 |
37.950 |
-8.883 |
1977 - 2022 |
82% |
|
|
ST JEAN DE LUZ |
469 |
43.395 |
-1.682 |
1942 - 2021 |
57% |
|